[最优化]无约束优化

最优化
12k words

0. 几种优化算法关系

1. 梯度法（Gradient Descent）

1.1 原理

  1. 目标函数的梯度：

    梯度法基于目标函数的梯度信息进行迭代优化。对于目标函数 ，梯度 表示了函数在某点 处的变化率和变化方向。梯度的方向是函数增长最快的方向，而梯度的负方向则是函数下降最快的方向。

  2. 迭代更新规则：

    梯度法通过迭代更新当前解 的值，使其朝着目标函数下降的方向移动。更新规则通常如下所示： 其中， 是第 步的解， 是下一步的解， 是学习率（也称为步长，为一个常数），控制了每一步迭代中移动的距离。

  3. 梯度法实际上是一个最朴素的算法，是后续很多算法的基石

1.2 算法步骤

  1. 初始化参数：选择合适的初始参数值

  2. 计算梯度：计算目标函数关于参数的梯度 。

  3. 更新参数：根据梯度的反方向调整参数值，更新参数 ，以减小目标函数的值。更新规则为：

    其中， 是学习率（步长），控制参数更新的幅度。

  4. 收敛判断：判断是否满足停止条件，例如达到最大迭代次数、目标函数值变化小于阈值等。

  5. 迭代：若未满足停止条件，则重复步骤 2-4，直到满足停止条件为止。

1.3 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

%matplotlib inline
%config InlineBackend.figure_format = 'svg'
plt.rc('text', usetex=True)

# 定义函数
def f(x):
    x_1, x_2, x_3 = x
    return (x_1 - 4)**4 + (x_2 - 3)**2 + 4*(x_3 + 5)**4

# 定义函数导数
def df_dx(x):
    x_1, x_2, x_3 = x
    df_dx1 = 4 * (x_1 - 4)**3
    df_dx2 = 2 * (x_2 - 3)
    df_dx3 = 16 * (x_3 + 5)**3
    return np.array([df_dx1, df_dx2, df_dx3])

# 初始点
x0 = np.array([4.0, 2.0, -1.0])

# 梯度下降法
def gradient_descent(f, df_dx,x0, learning_rate=0.005, epsilon=1e-6, max_iters=1000):
    x = x0
    recorder = list()
    recorder.append([0,x,0,f(x)])

    for i in range(max_iters):
        gradient = df_dx(x)
        if np.linalg.norm(gradient) < epsilon:
            break
        x = x - learning_rate * gradient
        recorder.append([i+1,x,gradient,f(x)])

    return x, pd.DataFrame(recorder, columns=['STEP', 'X','gradient', 'F(X)'])

# 求解
x_opt_gd,recorder_gd = gradient_descent(f,df_dx, x0)
print("Gradient Descent:")
print("Optimal Point:", x_opt_gd)
print("Minimum Value of f:", f(x_opt_gd))

recorder_gd

2. 最速法（Steepest Descent）

2.1 原理

最速法其实与梯度法非常非常类似，唯一区别在于最速法的步长是动态变化的，而非梯度法中的常数。最速法中的每一次迭代需要通过线性搜索算法重新计算步长。

本质：

  • 最速法是梯度法的一种实现

  • 是用线性函数去近似目标函数

    最速下降法可以被解释为在每一步迭代中使用当前点处的线性函数（梯度）来近似目标函数，并沿着该线性函数的反方向进行搜索

优点：

  1. 迭代过程简单，计算量和存储量小；

  2. 算法开局时函数值一般下降的很快，可以很快的靠近最优解的邻域。

缺点：

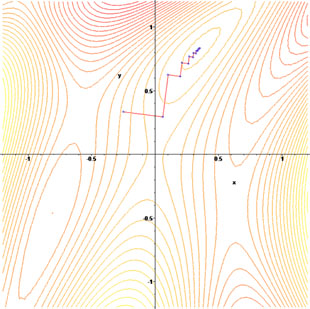
  1. 相邻两次迭代方向的正交性 (精准线性搜索定理) 导致锯齿现象，不适用于算法收敛。

2.2 算法步骤

  1. 初始化：

    • 选择初始点
    • 设定停止条件
    • 最大迭代次数

  2. 计算梯度：

  3. 更新参数：

    其中， 是学习率（步长），利用一维搜索确定

  4. 收敛判断：

    • 若 小于预先设定的阈值 ，则停止迭代
    • 若 达到最大迭代次数，则也停止迭代

  5. 迭代： 重复2-4

3.3 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

%matplotlib inline
%config InlineBackend.figure_format = 'svg'
plt.rc('text', usetex=True)

# 定义函数
def f(x):
    x_1, x_2, x_3 = x
    return (x_1 - 4)**4 + (x_2 - 3)**2 + 4*(x_3 + 5)**4

# 定义函数导数
def df_dx(x):
    x_1, x_2, x_3 = x
    df_dx1 = 4 * (x_1 - 4)**3
    df_dx2 = 2 * (x_2 - 3)
    df_dx3 = 16 * (x_3 + 5)**3
    return np.array([df_dx1, df_dx2, df_dx3])

# 初始点
x0 = np.array([4.0, 2.0, -1.0])

# Armijo条件线搜索，用来找到一个合适的步长
def line_search(f, df, x, d):
    alpha = 0.1
    beta = 0.5
    t = 1
    while f(x + t*d) > f(x) + alpha * t * np.dot(df(x), d):
        t = beta * t
    return t

# 最速下降法
def steepest_descent(f, df_dx, x0, epsilon=1e-6, max_iters=1000):
    x = x0
    recorder = list()
    recorder.append([0,x,0,0,f(x)])

    for i in range(max_iters):
        grad = df_dx(x)
        if np.linalg.norm(grad) < epsilon:
            break
        direction = -grad
        step_size = line_search(f, df_dx, x, direction)
        x = x + step_size * direction
        recorder.append([i+1,x,direction,step_size,f(x)])
    else:
        Warning("达到最大迭代次数，未能收敛")
    return x, pd.DataFrame(recorder, columns=['STEP', 'X', 'direction','step_size','F(X)'])

x_opt_sd, recorder_sd = steepest_descent(f, df_dx, x0)
print("Steepest Descent:")
print("Optimal solution:", x_opt_sd)
print("Optimal value of f(x):", f(x_opt_sd))

# 迭代过程
show_path(recorder_sd, "Steepest Descent Path")

3.牛顿法（Newton Method）

3.1 原理

由于最速下降法速度慢，Newton引入二阶梯度加速，通过求其Hesse矩阵，一步到位直接求到极小点

牛顿法的原理是基于使用一个二次函数去近似目标函数，然后精确地求出这个二次函数的极小点作为新的迭代点，从而逐步优化目标函数的过程

  1. 二次函数的选取：牛顿法通过在当前点处使用目标函数的二阶泰勒展开式来构建一个二次函数作为近似。在点 处，目标函数 的二阶泰勒展开式为：

    其中， 是目标函数在 处的梯度， 是目标函数在 处的Hessian矩阵。

  2. 迭代方向的选取：牛顿法的关键在于求解二次函数 的极小点，作为下一步迭代的方向。通过令二次函数的一阶导数为零，即 ，解出极小点所对应的 值，即为牛顿方向。

  3. 迭代更新：一旦求得牛顿方向 ，将其应用于当前点 ，即 ，得到下一次迭代的点 。

  4. 收敛性：如果初始点选择得当，且目标函数在局部区域内表现得足够光滑，那么牛顿法往往能够快速收敛到局部极小值点。这是因为牛顿法具有至少二阶收敛速度，即每次迭代都会更快地逼近极小值点。

总结，牛顿法利用二次函数近似目标函数，并通过精确求解二次函数的极小点来指导迭代方向，以加速目标函数的优化过程。

  • 缺点：
  1. 可能不正定，导致 可能不是下降方向
  2. 可能是奇异的，导致 无解
  3. 计算量过大

3.2 算法步骤

  1. 初始化：

    • 选择初始点 。
    • 设置精度参数 ，用于控制算法收敛的条件。
    • 初始化迭代次数 。

  2. 迭代过程：

    • 计算梯度和Hessian矩阵：
      • 计算目标函数在当前点 处的梯度 。
      • 计算目标函数在当前点 处的Hessian矩阵 。
    • 解牛顿方程：
      • 计算牛顿方向 。
    • 更新参数：
      • 更新迭代点：。

  3. 判断停止条件：

    • 如果 ，则算法收敛，停止迭代。
    • 否则，将 更新为 ，并回到步骤2。

3.3 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import numpy as np

# 定义目标函数
def f(x):
    return (x[0] - 4)**4 + (x[1] - 3)**2 + 4*(x[2] + 5)**4

# 初始点
x0 = np.array([3.9, 2, -1])

# 黑塞矩阵
def hessian(x):
    hessian_matrix = np.zeros((len(x), len(x)))
    # 计算二阶偏导数
    hessian_matrix[0, 0] = 12*(x[0] - 4)**2
    hessian_matrix[1, 1] = 2
    hessian_matrix[2, 2] = 96*(x[2] + 5)**2
    return hessian_matrix

# 牛顿法
def newton_method(f, x0, max_iter=1000, tol=1e-6):
    x = x0
    for _ in range(max_iter):
        gradient = approx_fprime(x, f, epsilon=1e-6)
        hess = hessian(x)
        step = np.linalg.solve(hess, -gradient)
        x = x + step
        if np.linalg.norm(step) < tol:
            break
    return x

print("牛顿法")
x_min_newton = newton_method(f, x0)
print("最小值点 ：", x_min_newton)
print("最小值   ：", f(x_min_newton))
  • 使用有限差分计算黑塞矩阵实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import numpy as np

# 定义目标函数
def f(x):
    return (x[0] - 4)**4 + (x[1] - 3)**2 + 4*(x[2] + 5)**4

# 初始点
x0 = np.array([3.9, 2, -1])

# 黑塞矩阵
def approx_hess(x, func, epsilon=1e-10):
    n = len(x)
    hessian = np.zeros((n, n))
    # 遍历计算海森矩阵的每个元素
    for i in range(n):
        for j in range(n):
            # 计算对x[i]和x[j]的一阶偏导数
            f_xi_xj_plus = func(x + epsilon * (np.eye(n)[i] + np.eye(n)[j]))
            f_xi_plus = func(x + epsilon * np.eye(n)[i])
            f_xj_plus = func(x + epsilon * np.eye(n)[j])
            # 使用二点有限差分计算二阶偏导数
            hessian[i, j] = (f_xi_xj_plus - f_xi_plus - f_xj_plus + func(x)) / (epsilon**2)
    return hessian

# 牛顿法
def newton_method(f, x0, max_iter=1000, tol=1e-6):
    x = x0
    for _ in range(max_iter):
        gradient = approx_fprime(x, f, epsilon=1e-6)
        hessian = approx_hess(x, f, epsilon=1e-6)
        step = np.linalg.solve(hessian, -gradient)
        x = x + step
        if np.linalg.norm(step) < tol:
            break
    return x

print("牛顿法")
start_time = time.time()
x_min_newton = newton_method(f, x0)
end_time = time.time()
print("最小值点 ：", x_min_newton)
print("最小值   ：", f(x_min_newton))
print("耗时     ：", end_time - start_time, "秒")

3.拟牛顿法（Quasi-Newton Methods）

3.1 前言

由于牛顿法存在

  1. 可能不正定，导致 可能不是下降方向
  2. 可能是奇异的，导致 无解
  3. 计算量过大

的缺点，针对 的各项问题，提出利用一个近似矩阵 来替代 。

近似矩阵 需要满足：

  2. 对称正定
  3. 计算更加简单

3.2 SR1

3.2.1 基本信息

  • 名称：Symmetric Rank-One
  • 提出者：William C. Davidon
  • 时间：1956年

  • 其中:

3.2.2 推导

待补充....

3.2.3 算法步骤

  1. 初始令

  2. 计算梯度：

  3. 计算搜索方向：

  4. 更新参数：

    • 更新迭代点：
    • 更新矩阵：

  5. 判断停止条件：

    • 如果 ，则算法收敛，停止迭代
    • 否则，将 更新为 ，并回到步骤 2

3.2.4 收敛性

超线性收敛

虽然不是一般的超线性，但是依然算是超线性的收敛速度（准确来说是n+1 步Q-超线性收敛速度

3.2.5 代码实现

注意此处实际上是阻尼拟牛顿法的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import numpy as np
from scipy.optimize import approx_fprime
import time

# 定义目标函数
def f(x):
    return (x[0] - 4)**4 + (x[1] - 3)**2 + 4*(x[2] + 5)**4

# 初始点
x0 = np.array([3.9, 2, -1])

# 线搜索（使用Armijo准则）
def line_search(f, xk, pk, alpha=1, beta=0.5, c=0.1):
    while f(xk + alpha * pk) > f(xk) + c * alpha * np.dot(approx_fprime(xk, f, epsilon=1e-6), pk):
        alpha *= beta
    return alpha

# Rank-1更新的拟牛顿法
def rank1_method(f, x0, max_iter=1000, tol=1e-6):
    n = len(x0)
    Hk = np.eye(n)  # 初始Hessian逆估计
    xk = x0
    gk = approx_fprime(xk, f, epsilon=1e-6)  # 初始梯度估计
    for k in range(max_iter):
        pk = -np.dot(Hk, gk)  # 计算搜索方向
        alpha = line_search(f, xk, pk)  # 使用线搜索确定步长
        x_next = xk + alpha * pk  # 更新参数
        g_next = approx_fprime(x_next, f, epsilon=1e-6)
        sk = x_next - xk
        yk = g_next - gk
        if np.linalg.norm(yk) < tol:
            break
        # Rank-1更新Hessian逆估计
        Hk += np.outer(sk - np.dot(Hk, yk), sk) / np.dot(sk - np.dot(Hk, yk), yk)
        xk = x_next
        gk = g_next
    return xk

print("rank1-拟牛顿法")
start_time = time.time()
x_min_rank1 = rank1_method(f, x0)
end_time = time.time()
print("最小值点 ", x_min_rank1)
print("最小值   ：", f(x_min_rank1))
print("耗时     ：", end_time - start_time, "秒")

3.3 DFP

3.3.1 基本信息

  • 名称：Davidon-Fletcher-Powell
  • 提出者：Davidon、Fletcher、Powell
  • 时间：1969年

  • 其中:

3.3.2 推导

待补充....

3.3.3 算法步骤

  1. 初始令

  2. 计算梯度：

  3. 计算搜索方向：

  4. 更新参数：

    • 更新迭代点：
    • 更新矩阵：

  5. 判断停止条件：

    • 如果 ，则算法收敛，停止迭代
    • 否则，将 更新为 ，并回到步骤 2

3.3.4 收敛性

收敛性证明目前空缺

3.3.5 代码实现

注意此处实际上是阻尼拟牛顿法的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import numpy as np
from scipy.optimize import approx_fprime
import time

# 定义目标函数
def f(x):
    return (x[0] - 4)**4 + (x[1] - 3)**2 + 4*(x[2] + 5)**4

# 初始点
x0 = np.array([3.9, 2, -1])

# 线搜索（使用Armijo准则）
def line_search(f, xk, pk, alpha=1, beta=0.5, c=0.1):
    while f(xk + alpha * pk) > f(xk) + c * alpha * np.dot(approx_fprime(xk, f, epsilon=1e-6), pk):
        alpha *= beta
    return alpha

# DFP算法
def DFP_method(f, x0, max_iter=1000, tol=1e-6):
    n = len(x0)
    Hk = np.eye(n)  # 初始Hessian逆估计
    xk = x0
    gk = approx_fprime(xk, f, epsilon=1e-6)  # 初始梯度估计
    for k in range(max_iter):
        pk = -np.dot(Hk, gk)  # 计算搜索方向
        alpha = line_search(f, xk, pk)  # 使用线搜索确定步长
        x_next = xk + alpha * pk  # 更新参数
        g_next = approx_fprime(x_next, f, epsilon=1e-6)
        sk = x_next - xk
        yk = g_next - gk
        if np.linalg.norm(yk) < tol:
            break
        # 更新Hessian逆估计
        Hk = Hk + np.outer(sk, sk) / np.dot(sk, yk) - np.dot(np.outer(np.dot(Hk, yk), sk), Hk) / np.dot(np.dot(yk, Hk), yk)
        xk = x_next
        gk = g_next
    return xk

print("DFP-拟牛顿法")
start_time = time.time()
x_min_DFP = DFP_method(f, x0)
end_time = time.time()
print("最小值点 ", x_min_DFP)
print("最小值   ：", f(x_min_DFP))
print("耗时     ：", end_time - start_time, "秒")

3.4 BFGS

3.4.1 基本信息

  • 名称：Broyden-Fletcher-Goldfarb-Shanno
  • 提出者：Broyden、Fletcher、Goldfarb和Shanno
  • 时间：1970年

  • 其中:

3.4.2 推导

待补充....

3.4.3 算法步骤

是的就更新矩阵部分变了，其余一样

  1. 初始令

  2. 计算梯度：

  3. 计算搜索方向：

  4. 更新参数：

    • 更新迭代点：
    • 更新矩阵：

  5. 判断停止条件：

    • 如果 ，则算法收敛，停止迭代
    • 否则，将 更新为 ，并回到步骤 2

3.4.4 收敛性

Q-超线性收敛速度

3.4.5 代码实现

注意此处实际上是阻尼拟牛顿法的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import numpy as np
from scipy.optimize import approx_fprime
import time

# 定义目标函数
def f(x):
    return (x[0] - 4)**4 + (x[1] - 3)**2 + 4*(x[2] + 5)**4

# 初始点
x0 = np.array([3.9, 2, -1])

# 线搜索（使用Armijo准则）
def line_search(f, xk, pk, alpha=1, beta=0.5, c=0.1):
    while f(xk + alpha * pk) > f(xk) + c * alpha * np.dot(approx_fprime(xk, f, epsilon=1e-6), pk):
        alpha *= beta
    return alpha

# BFGS算法
def BFGS_method(f, x0, max_iter=1000, tol=1e-6):
    n = len(x0)
    Hk = np.eye(n)  # 初始Hessian逆估计
    xk = x0
    gk = approx_fprime(xk, f, epsilon=1e-6)  # 初始梯度估计
    for k in range(max_iter):
        pk = -np.dot(Hk, gk)  # 计算搜索方向
        alpha = line_search(f, xk, pk)  # 使用线搜索确定步长
        x_next = xk + alpha * pk  # 更新参数
        g_next = approx_fprime(x_next, f, epsilon=1e-6)
        sk = x_next - xk
        yk = g_next - gk
        if np.linalg.norm(yk) < tol:
            break
        # 更新Hessian逆估计
        rho_k = 1.0 / np.dot(yk, sk)
        A1 = np.eye(n) - rho_k * np.outer(sk, yk)
        A2 = np.eye(n) - rho_k * np.outer(yk, sk)
        Hk = np.dot(np.dot(A1, Hk), A2) + rho_k * np.outer(sk, sk)
        xk = x_next
        gk = g_next
    return xk, f(xk)

print("BFGS-拟牛顿法")
start_time = time.time()
x_min_BFGS, min_value = BFGS_method(f, x0)
end_time = time.time()
print("最小值点 ", x_min_BFGS)
print("最小值   ：", f(x_min_BFGS))
print("耗时     ：", end_time - start_time, "秒")

参考

  1. https://zhuanlan.zhihu.com/p/538910657
  2. https://zhuanlan.zhihu.com/p/306635632
  3. https://zhuanlan.zhihu.com/p/338829644
  4. https://zhuanlan.zhihu.com/p/144736223