[最优化]线性搜索

最优化
6k words

1.直接搜索

1.1 黄金分割法

1.1.1 基本信息

  • 适用范围：单峰函数求极小值问题

  • 特点：

    1. 迭代逼近极小值点：

      黄金分割法通过不断地迭代，在每一步中缩小搜索区间，以逼近极小值点。每次迭代都会根据黄金比例将当前搜索区间分成两部分，并选择较小函数值所在的部分进行下一步的搜索。

    2. 不依赖梯度信息：

      与梯度下降方法不同，黄金分割法不需要函数的梯度信息。它是一种无梯度的优化方法，适用于那些无法或难以求得梯度信息的问题。

  • 基本原理：

    黄金分割法是建立在区间消去法原理基础上的试探方法，即在搜索区间[a,b]内适当插入两点a1, a2，并计算其函数值。

    a1, a2将区间分成三段，应用函数的单峰性质，通过函数值大小的比较，删去其中一段，是搜索区间得以缩小。然后再在保留下来的区间上作同样的处理，如此迭代下去，搜索区间无限缩小，从而得到极小点的数值近似解。

1.1.2 算法流程

  1. 初始化：

  2. 计算内部点：

    黄金比例：

  3. 计算函数值：

  4. 选择新区间：

    如果否则

    如果否则

  5. 收敛判断：

    如果满足停止迭代条件，则停止迭代；否则，增加迭代次数 ，返回步骤 2 继续迭代。

1.1.3 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import math

%matplotlib inline
%config InlineBackend.figure_format = 'svg'
plt.rc('text', usetex=True)
plt.rc('font', family='serif')

# 定义函数
def f(x):
    return x**2 + 4 * np.cos(x)

# 黄金分割法
def golden_section(f, a, b, tol=1e-5):
    # 黄金分割比例
    golden_ratio = (math.sqrt(5) - 1) / 2
    # 初始区间长度
    length = b - a
    # 计算初始内点
    x1 = b - golden_ratio * length
    x2 = a + golden_ratio * length
    # 计算函数值
    f1 = f(x1)
    f2 = f(x2)
    # 记录最小值所在的 x
    min_x = None
    min_f = None
    
    # 创建表格记录每一步的值
    steps = pd.DataFrame(columns=['a', 'b', 'x1', 'x2', 'f(x1)', 'f(x2)', 'New uncertainty interval'])

    # 迭代直至达到收敛条件
    step = 0
    while length > tol:
        # 计算新的不确定性区间
        new_interval = (a, b)
        steps.loc[step] = [a, b, x1, x2, f1, f2, new_interval]
        
        if f1 < f2:
            b = x2
            x2 = x1
            x1 = b - golden_ratio * (b - a)
            f2 = f1
            f1 = f(x1)
        else:
            a = x1
            x1 = x2
            x2 = a + golden_ratio * (b - a)
            f1 = f2
            f2 = f(x2)
        length = b - a
        if min_f is None or f1 < min_f:
            min_f = f1
            min_x = x1
        step += 1

    return min_x, steps 

# 使用黄金分割法寻找最小值
min_x_gold,steps_gold = golden_section(f, 1, 2,1e-3)

# 输出结果
print("函数的最小值在 x =", min_x_gold)
print("函数的最小值为:", f(min_x_gold))

print("\n迭代步骤:")
steps_gold

1.2 斐波那契搜索

  • 适用范围：单峰函数求极小值问题

  • 特点：

    • 与1黄金分割法类似

1.2.1 对比

  • Fibonacci法

    • 计算次数确定: 在使用Fibonacci法之前，需要根据目标精度预先计算出检查函数值的次数。这通常涉及到选择一个足够小的Fibonacci数作为最终区间长度的目标，从而反推出。

    • 优点: 能够确保原始区间与最终选定区间长度的比值接近最优（即最大值），这是由于Fibonacci序列的性质决定的。

    • 缺点: 每次区间缩短的比例是变化的，这可能导致计算过程相对复杂且计算量较大，尤其是在确定迭代步数时。

  • 黄金分割法

    • 作为极限形式: 黄金分割法可视作Fibonacci法的一种简化或极限情况，其区间缩短率固定为黄金比例0.618。

    • 缩短率计算: 黄金分割法中，每次迭代都保持区间被分割的比例不变，即保留的两部分和长度比约为黄金比例分割。这一比例由下式体现：，当取时，满足黄金分割的要求，使得区间缩小的方式达到一种平衡状态，既高效又稳定。

  • 总结

    Fibonacci法提供了理论上最优的区间缩小策略，但实施起来较为复杂。相比之下，黄金分割法则通过固定分割比率简化了计算过程，虽然可能不是最优的区间缩小比例分配，但其简单性和实用性使其成为寻找函数极值点的常用方法之一。

1.2.2 算法流程

  1. 初始化斐波那契数列的前两个元素：

  2. 计算搜索区间长度，其中 和 为区间端点，

  3. 计算斐波那契数列长度n

    • ，其中为搜索区间的长度，为给定的精度。

  4. 计算内点和：

    • 。

  5. 计算和

  6. 比较和，更新搜索区间

    • 如果，则新的搜索区间为。
    • 如果，则新的搜索区间为。
    • 如果，则新的搜索区间为。

  7. 重复步骤4到步骤6，直到搜索区间的长度小于给定的精度

1.2.3 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
# 计算斐波那契数列的前 n 项
def fibonacci(n):
    if n <= 0:
        return [0]
    elif n == 1:
        return [0, 1]
    else:
        fib = [0, 1]
        for i in range(2, n + 1):
            fib.append(fib[i - 1] + fib[i - 2])
        return fib

def fibonacci_search(func, a, b, tol=1e-5):
    # 计算斐波那契数列的项数，直到满足精度要求
    n = 2
    while (b - a) / fibonacci(n)[-1] > tol:
        n += 1

    # 创建列表记录每一步的值
    steps_list = []

    # 获取斐波那契数列的前 n 项
    fib = fibonacci(n)
    # 根据斐波那契数列的比例划分闭区间
    x1 = a + (b - a) * fib[n - 2] / fib[n]
    x2 = a + (b - a) * fib[n - 1] / fib[n]

    # 计算函数在划分的两个点处的值
    f1 = func(x1)
    f2 = func(x2)

    # 在剩余的 n-2 个区间中搜索
    for i in range(1, n - 2):
        if f1 < f2:
            # 如果第一个点的函数值更小，则将区间右端点移动到第二个点处
            b = x2
            x2 = x1
            # 重新计算第一个点的位置
            x1 = a + (b - a) * fib[n - i - 2] / fib[n - i]
            f2 = f1
            f1 = func(x1)
        else:
            # 如果第二个点的函数值更小，则将区间左端点移动到第一个点处
            a = x1
            x1 = x2
            # 重新计算第二个点的位置
            x2 = a + (b - a) * fib[n - i - 1] / fib[n - i]
            f1 = f2
            f2 = func(x2)

        # 将每一步的值记录到列表中
        steps_list.append({'ρ_k': (b - a) / (b - a + (b - a) * fib[n - i] / fib[n - i + 1]),
                           'a_k': a,
                           'b_k': b,
                           'f(a_k)': f1,
                           'f(b_k)': f2,
                           'New uncertainty interval': [a, b]})

    # 将列表转换为 DataFrame
    steps = pd.DataFrame(steps_list)

    # 返回搜索到的最小值点及其函数值
    if f1 < f2:
        return x1, steps
    else:
        return x2, steps


min_x_fibonacci, steps = fibonacci_search(f, 1, 2,0.05)
print("最小值：", f(min_x_fibonacci))
print("最小值点：", min_x_fibonacci)
print("迭代步骤：")
steps

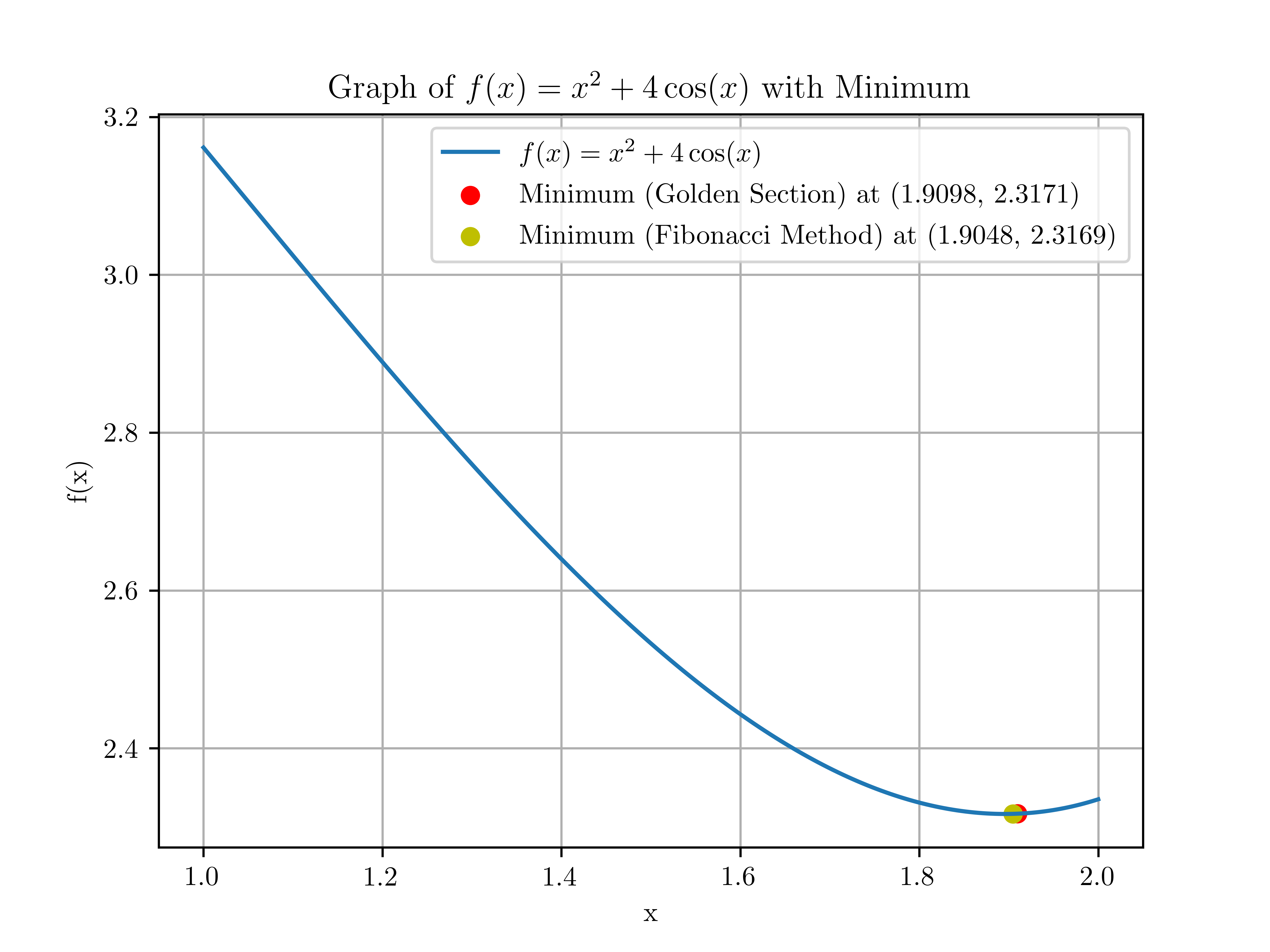
2.精确线搜索

2.1 目标

找到一个步长 使得

2.2 精确线搜索定理

  • 推导如下：

    在一个线性搜索中，给定搜索方向，

    目的是找到一个合适的使得，

    就是找到一个步长使函数值更加小。

    如果能找到一个最佳的步长使函数值最小，即

    称为精确线搜索。 既然找到的步长是最佳的，也就是最小的，则在处的梯度（对步长一阶导数）为0，即：

3.非精确线搜索

精确线搜索算法往往会需要很大的计算量，因此，我们一般青睐于非精确线搜索算法。

3.1 目标

找到一个步长，使

3.2 Armijoz准则

其中：

  • 是当前点 的目标函数值，
  • 是搜索方向，
  • 是步长，
  • 是一个控制参数，通常取值范围为

3.3 Goldstein准则

其中： - 是当前点 的目标函数值， - 是搜索方向， - 是步长， - 和 是两个控制参数，通常取值范围为 。

3.4 Wolfe准则

其中： - 是当前点 的目标函数值， - 是搜索方向， - 是步长， - 和 是两个控制参数，通常取值范围为 。

5.参考

  1. https://zhuanlan.zhihu.com/p/651901246
  2. https://blog.csdn.net/qq_37314249/article/details/104525944